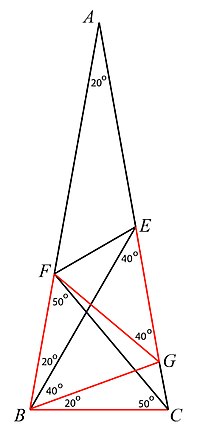
角度 を求める問題のときは、内心は 角の二等分線の交点 である、という特徴が活用できるよ。 IB,ICはそれぞれ 角の二等分線 だから、∠IBC=40°、∠ICB=25°とわかるね。 あとは、 IBCの内角の和 から、α=180°40°25°で求められるね。 (1)の答え三角形の外心の作図 現実事象をモデルとし、三角形の外心を作図することで、外心の理解を深め、 外心に興味をもち、単元の有用性を感じることが、この教材のねらいである。 図1のように、欠けてしまった円形のお皿がある。このお皿は古い時代のもので外心、傍心などの基本事項や 発展問題、補助線の練習 補助線の練習その1 正方形と正三角形を組み合わ せた角度の問題です。 ラングレーの問題 別名「整角四角形」「フランクリンの凧」 とか呼ばれる問題です。 面積の問題
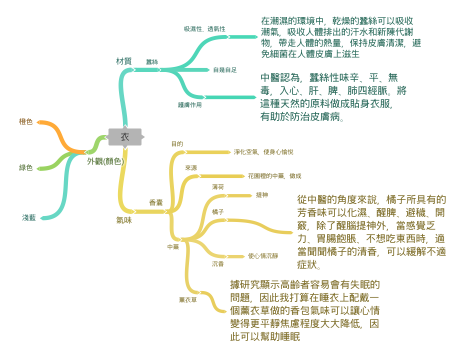
衣
外心 角度 問題
外心 角度 問題-問題自体はシンプルですが, かなりの難問です まず, 結ぶ線が特殊ですね 点\(e,f\)を結ぶのは考えづらいし, ましてや外心と傍心を結ぶなんてやばそうです 僕は, この問題が難しいとうわさで聞いていたので解こうとしたのですが全然わかりませんでした三角形の外心の性質 三角形の3つの辺それぞれの垂直二等分線は、1点で交わる。この点のことを三角形の外心という。 このテキストでは、この定理を証明します。 証明 ABCにおいて、辺ABの垂直二等分線と、辺ACの垂直二等分線の交
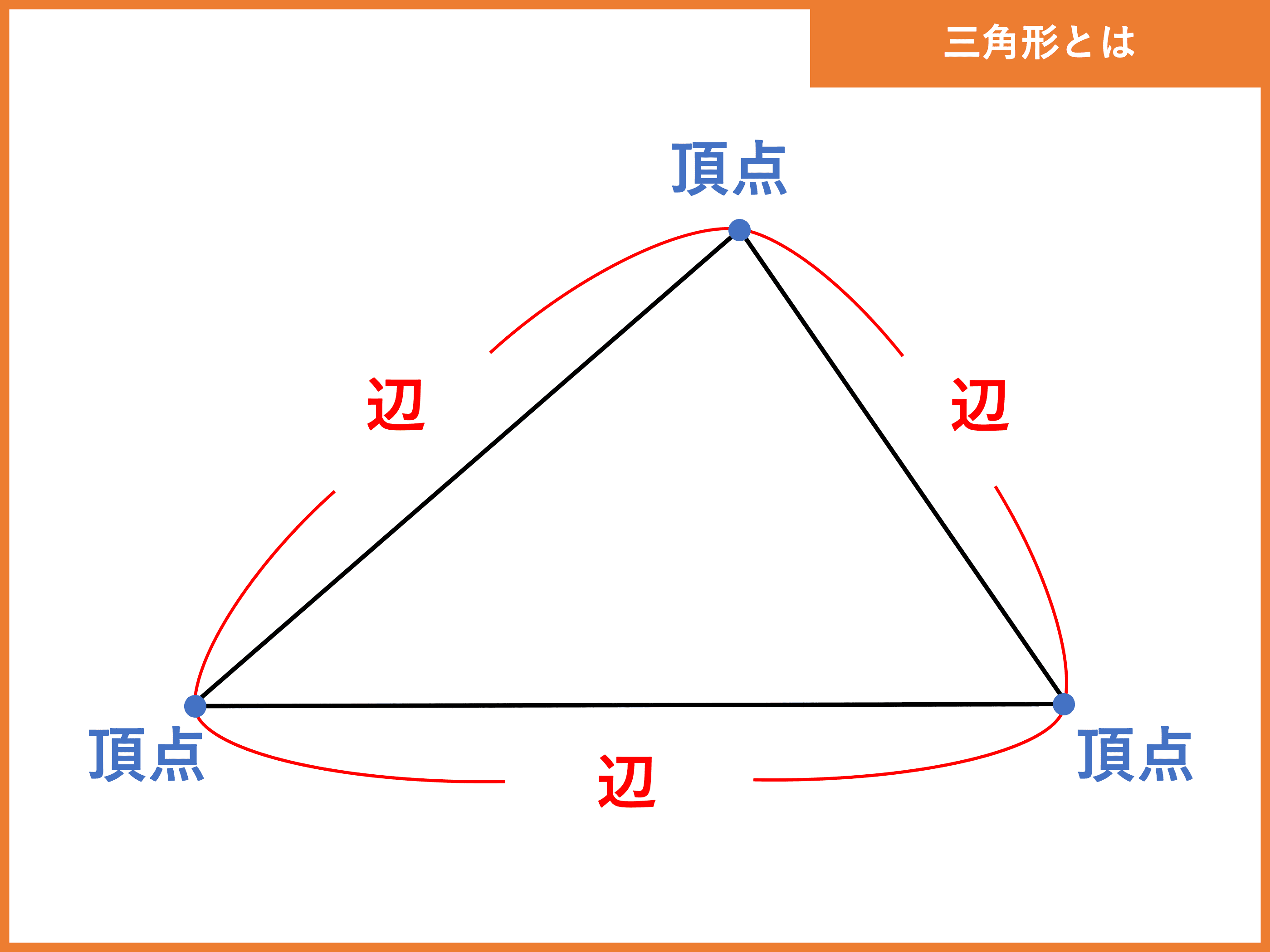


三角形とは 面積公式 角度 辺の長さ 重心 比の計算 受験辞典
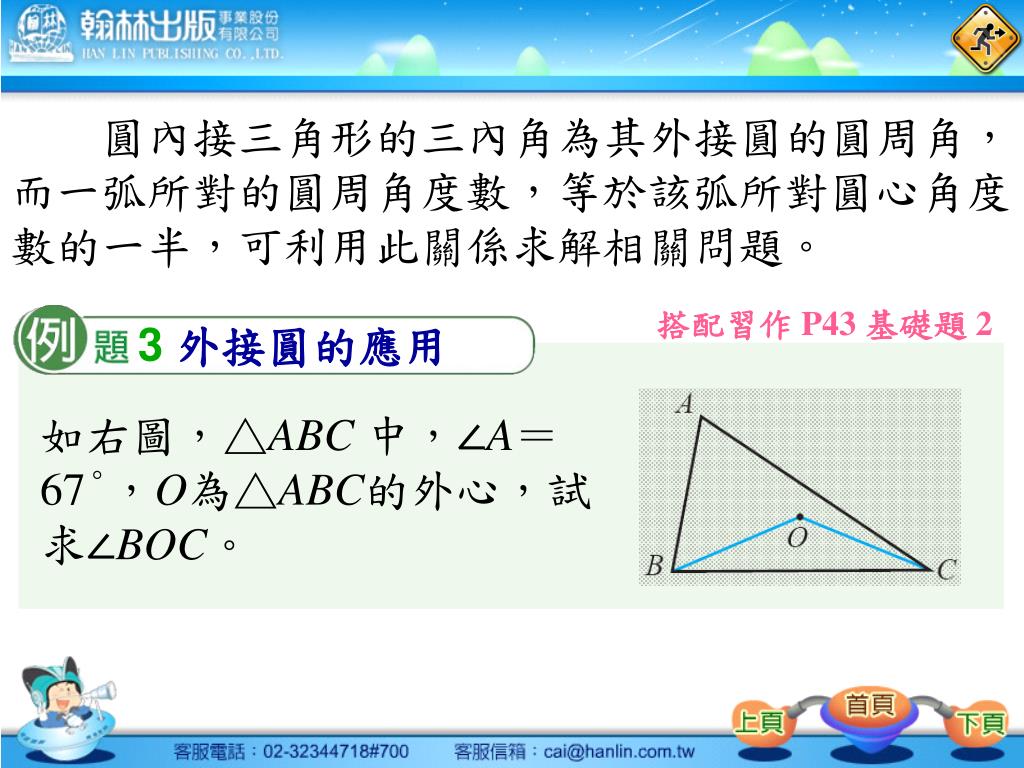
三角形OCAは正三角形。 また、線分AQは線分OCに垂直に接する。 愛知県 YMOjisan さんからの解答。 解答 12度 点P周りの角のうち2つが138度であることを利用して補助線CQを引くと、下図より、少なくとも12度という解が存在する。 なお図中、緑枠内数値は条件から直接得られる値で、 黄色枠は∠BAQ=6度の仮定から得られる値。 また、線分BPから始める作図の方法外心の性質を用いた応用問題3選 ここからは、外心の性質を用いた応用問題について見ていきましょう。 具体的には、 角度を求める問題;外心 我會利用尺規作圖找出三角形的外心。 外心 我會利用GeoGebra繪圖軟體畫出三角形的外心。 外心 我知道三角形三邊中垂線與外心的關係。 外心 我能透過三角形的外心事出30°60°90°的直角 ,三邊長的關係 外心 我能夠解決與三角形外心有關的角度問題。
角度の問題((30 a)°) 図において d は ⊿abc の頂点 a から 辺 bc に下ろした垂線の足とする。 ∠bad = (30 a)°, ∠cad = (60 a)°とする e は ad 上の点で ∠ace = (30 2a)°とする。このとき ∠ebc = 3a°であることを示せ。三角形の外心 三角形の各辺の垂直二等分線に関して以下の定理が成り立つ。 三角形の3つの辺の垂直二等分線は1点で交わり、その交点は3つの頂点から等距離にある。 これは一体どう意味であろうか? 実際に証明をしながら説明していこうと思う。 図1数学Aの角度を求める問題について教えて下さい。 問16) ABCの外心をO、垂心をHとする。∠OBC=40度のとき、∠A、及び∠BHCの大きさを求めよ。解)∠A=50度はでたのですが、どうして∠BHC=130度になるのかわかりません。解説よろしくお願い致します。 辺ABと直線CHの交点をDと置き、辺CAと直線BH
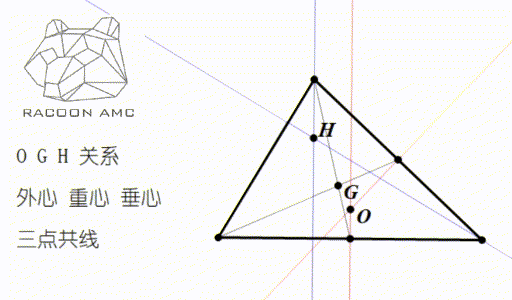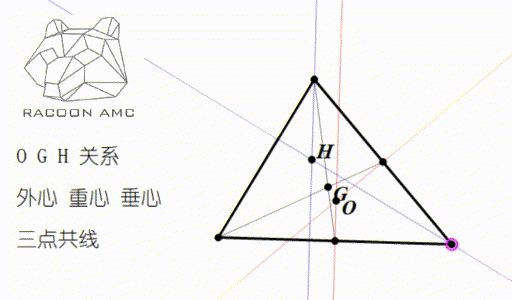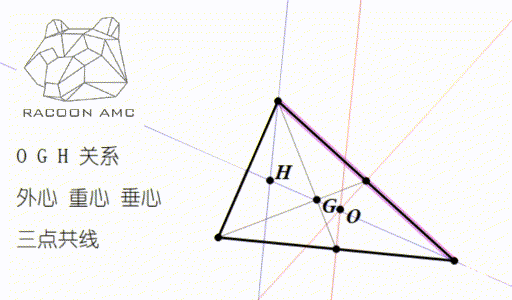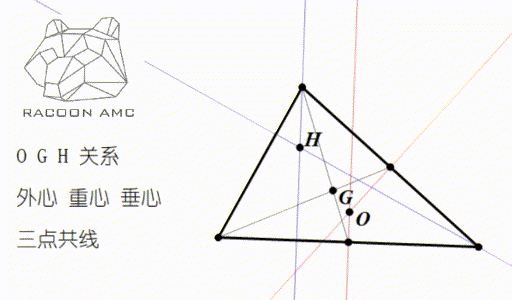
3/6/21 · 有名問題です。 tan \tan tan が整数なので各角度は 4 5 ∘ 45^{\circ} 4 5 ∘ 以上である。よって,三角形 A B C ABC A BC は鈍角三角形ではない。 よって, tan A, tan B, tan C \tan A,\tan B,\tan C tan A, tan B, tan C は正の整数である。外心の角度の関係 その1 ABCの外心Oをとして、外心O が ABCの内部にあるとき、外 接円の半径から、3つの二等辺 三角形がある。その底角を図の ようにa,b,c,とすると、 2a+2b+2c=180° 2でわっ外心,重心,垂心は1直線上にあることを示すことができる.(内心は,これら3点と同一直線上にあるとは限らない) (51)を直接示そうとすると, の 差 を比較することになるが,これらはすでに複雑な三角関数の分数式になっているので,通分などが容易



43yfj6tdwncofm



必修四向量 三角形 重心 垂心 內心 外心 向量結論與證明 每日頭條
な証明が続いたり、単調に長さや角度を求める問題 が多かったりなど、生徒の学習意欲が低下する場面 が多いように感じている。 そこで本論では、重心と外心についての生徒が興 味をもち学習意欲を高める発展的な教材とその授業 展開例を提案する。外心 辺の垂直二等分線、3 本の交点。 垂心 3 本の高さ(各頂点からその対辺へ垂直に下ろした線分)の交点。 傍心 三角形の傍接円の中心。1/18/17 · 三角形の内角 三角形の内角の和は \(180°\) である。 内角とは、内側の角のことですね。 三角形の \(3\) つの内角の大きさをすべて、足すと \(180°\) 、つまり一直線になるということです。 三角形がどんな形であっても成り立ちます。 この事実は当然の丸暗記なのですが、なぜ?


4个征兆可能是肝癌中医 这些症状是肝出问题了 晚期 耳朵 肝病 大纪元
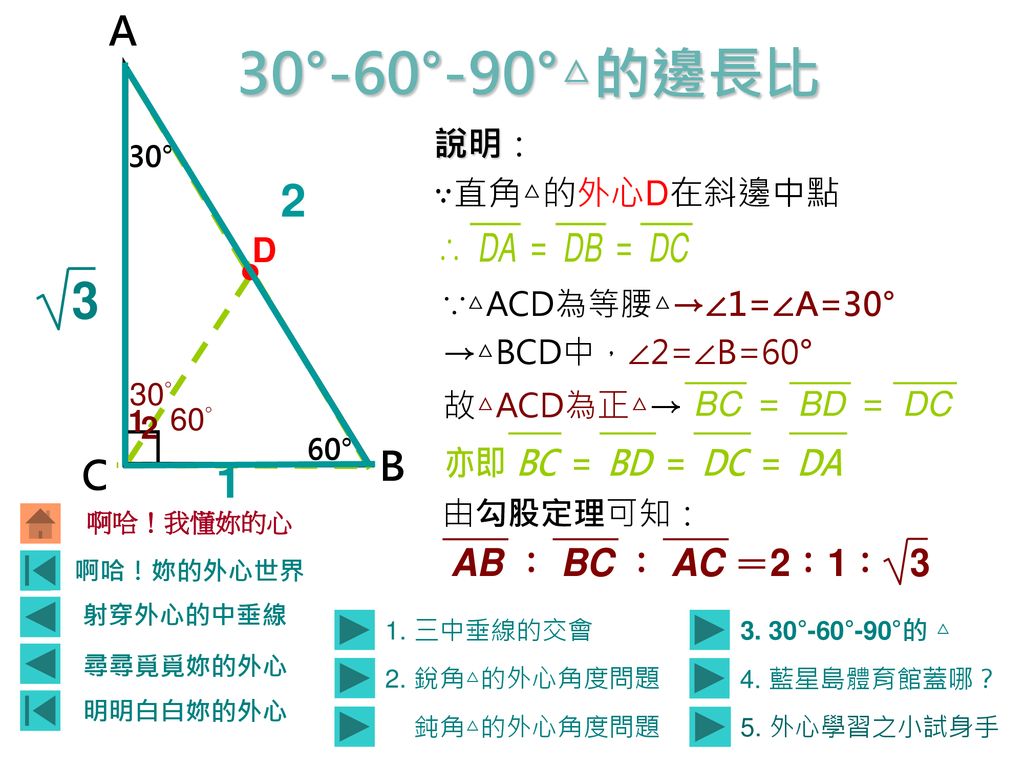


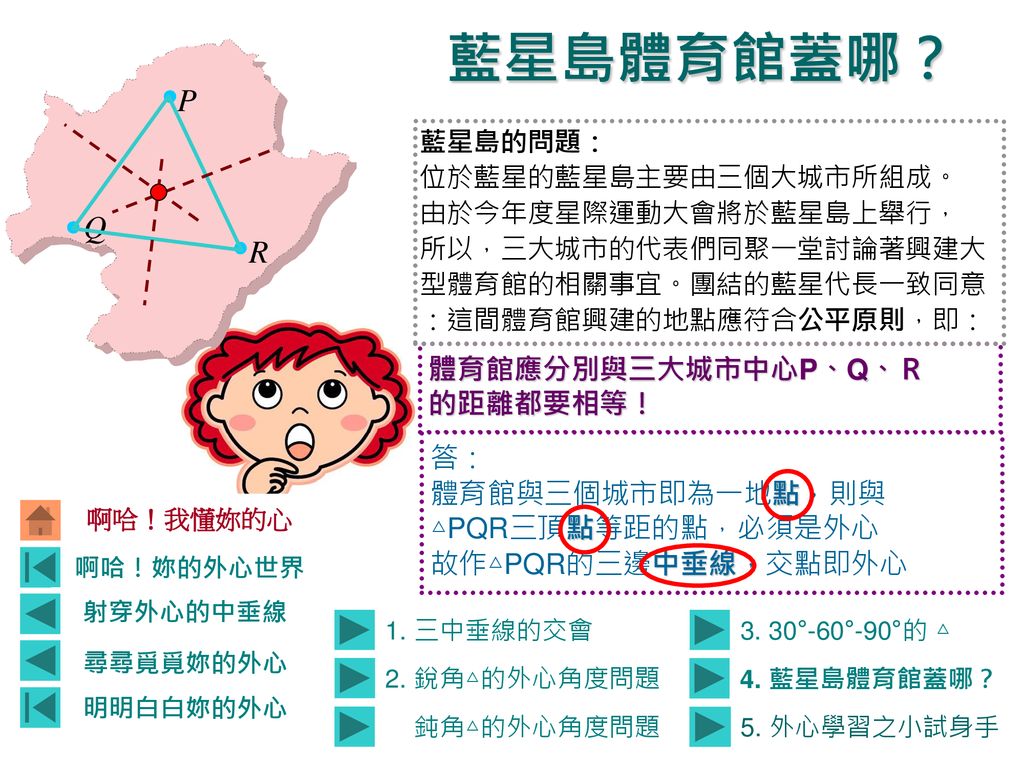
啊哈 妳的外心世界如果你能懂我的外心世界 你就能解決這個問題喔 這是藍星上的藍星島 島上的三個大城市
内心・外心 この問題は αの角度を求める問題なんですが、答えが115゜になる意味が解りません(*_*) 私は100゜だと思っていました; ちなみにIは abcの内心だそうです。 回答お願いします。外心 三角形の3辺の垂直二等分線は1点で交わる。 この点を外心という。 外心は3つの頂点から等距離にある。 (外接円の中心)2/28/11 · 数学・算数 この問題は αの角度を求める問題なんですが、答えが115゜になる意味が解りません(*_*) 私は100゜だと思っていました; ちなみにIは abcの内心だそうです。 回答お願いしま



8种方法解决一道三角形中角格点经典问题 题型虽老 但仍有价值 外接圆 外心 共圆 网易订阅


三角形とは 面積公式 角度 辺の長さ 重心 比の計算 受験辞典
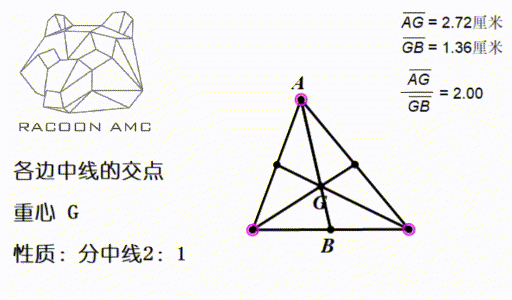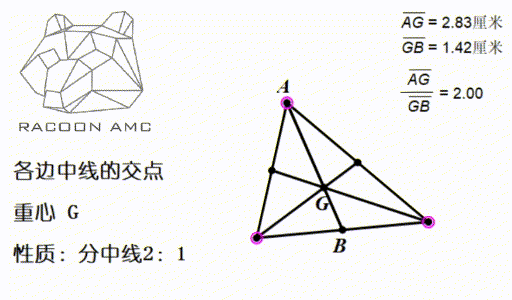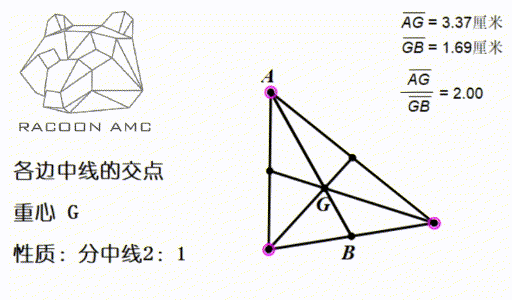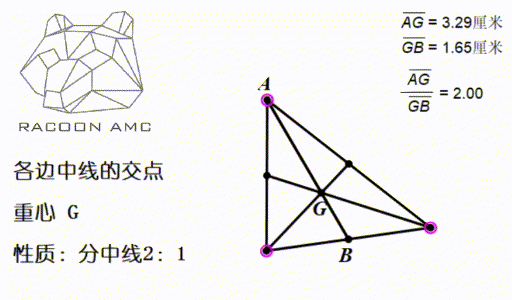
3/6/21 · 外心 定義:各辺の垂直二等分線の交点。 解析幾何的性質: ・外心の位置ベクトル o undefined \overrightarrow {o} o は各頂点の位置ベクトルを用いて以下のように表される: o undefined = sin 2 A a undefined sin 2 B b undefined sin 2 C c undefined sin 2 A sin 2 B sin 2 C \overrightarrow {o}=\dfrac {\sin 2A\overrightarrow {a}\sin 2B\overrightarrow {b}\sin外心、内心の基本問題 (角度) ABCの外心をOとする。 角α、βを求めよ。 α β 51° 19° O 答α=70°, β=° O β α 26° 40° 答α=100°, β=24° < O α β 41° 18° 答α=59°, β=118°数学a 授業プリント# 27 年 組 号 氏名 三角形の重心 b c a n m l g ☆ ☆ 2 2 1 1 2 1 㾻三角形の3 つの中線は、1 点で交わる。 この点 を重心という 㾼重心は、各中線を2 1 に内分する 例題1 右の三角形で点g は4abc の重心である。 このときbl、cg の長さを求めなさい。 b c a n m l g 3 cm
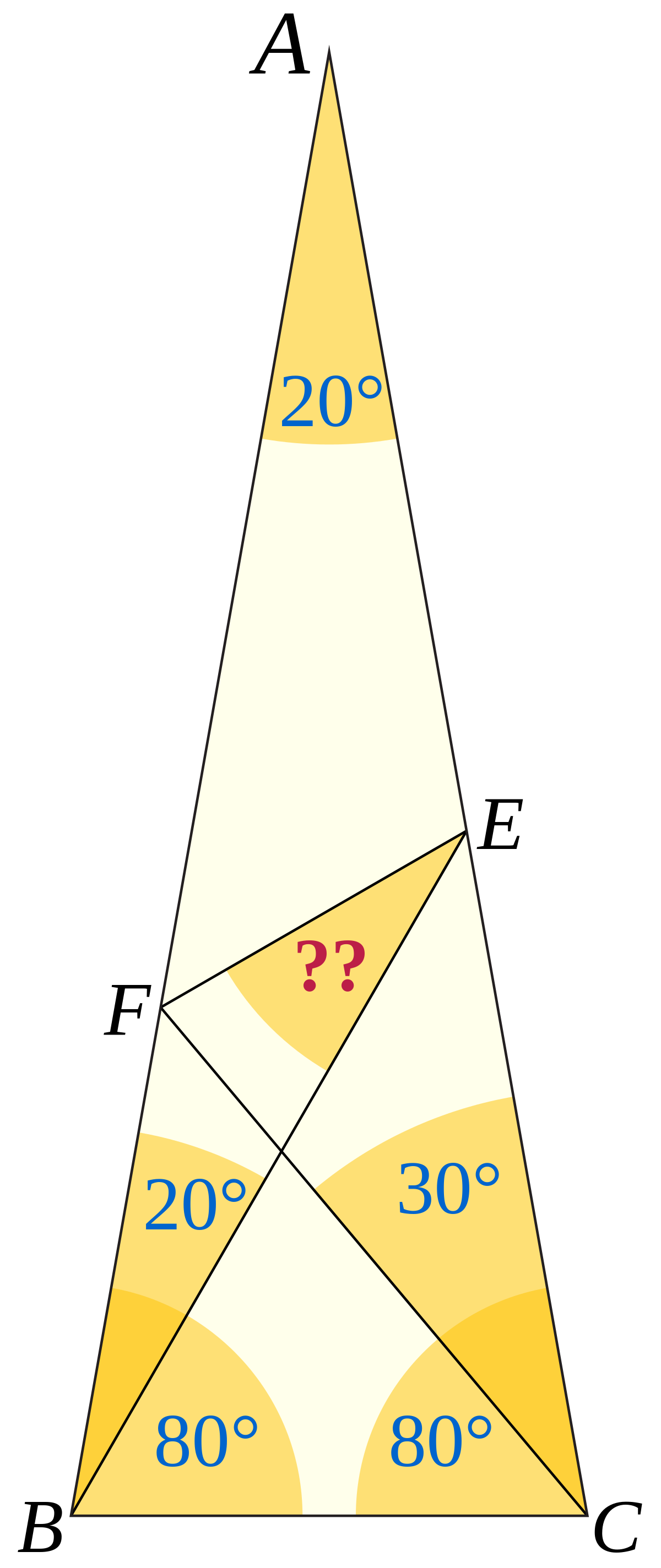


兰利的不定角度问题 维基百科 自由的百科全书


19中考数学试卷答案及考点分析
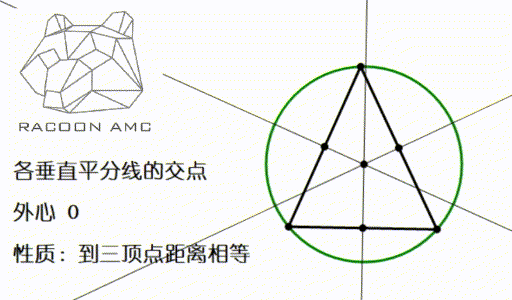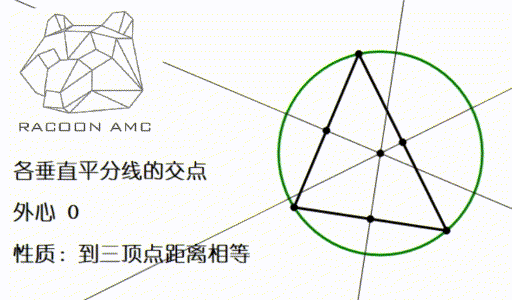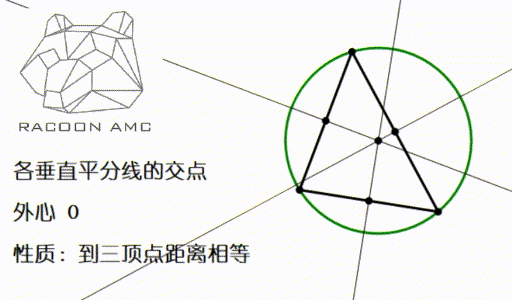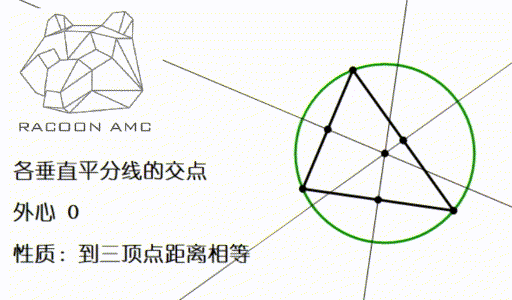
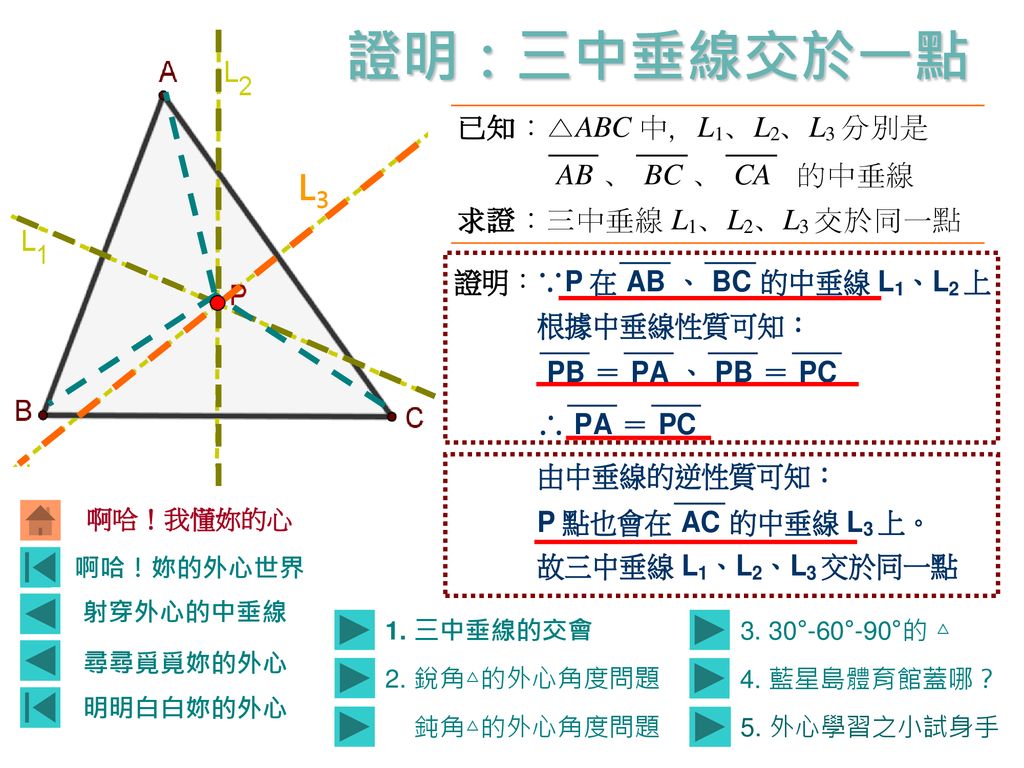
12/13/19 · 外心の特徴、問題の解き方 外心 とは、 外接円の中心 のことをいいます。 外接の円の中心、略して外心だね。 では、外心の特徴についてまとめておきましょう。 では、こられの特徴を使って問題を解いてみましょう。 問題 点Oは ABCの外心である。 このとき、 の大きさを求めなさい。 外心のときには、各頂点から外心に向かって補助線を引いてみましょう。11/24/ · 角$\alpha,\ \beta$を求めよ中心角と円周角の関係}より $ 外心に関する角度の問題では次の2点が重要である \\2zh \maru1\ \ \bm{外心と3頂点を結ぶと3つの二等辺三角形ができる} \\2zh \maru2\ \ \bm{補助円を描いて円の性質を利用する} \\1zh (1)\ \ とにかく二等辺三角形の3辺の垂直二等分線は、1点で交わり、その点から各頂点までの距離は等しい。 三角形の外心、三角形の外接円 この1点で交わった点 O を三角形の外心という。 外心 O を中心として、半径 OA の円が三角形 ABC の外接円である。 OA = OB = OC OL ⊥ BC 、 OM ⊥ AC 、 ON ⊥ AB
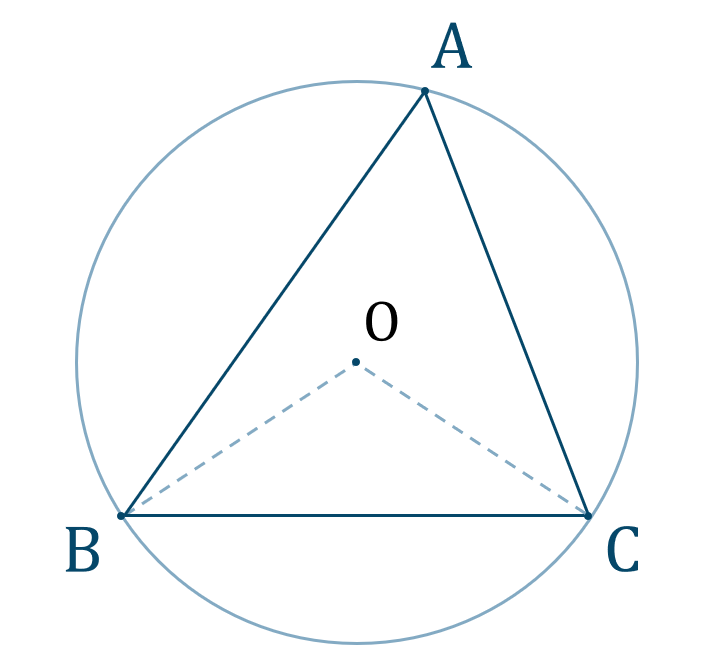


数学a 三角形の外心の性質の使い方とコツ 教科書より詳しい高校数学


心理学角度看医患沟通的三大难点
角度の問題 #36 解答例 ない」とされていた問題群の1つですが,15年10月にaerile_re氏によって全ての整角四角形問題に適用可能な証明方法が発見されたことにより,本問を含む問題群も初等幾何で証明可能となりました.その手法「外心3つ法」の詳細は為學日增 為道日損~ Sign in Recent Site Activity Report Abuse Print Page Powered By Google Sites Recent Site Activity Report Abuse Print Page Powered By Google Sites位置ベクトルを求める問題(数学b) この $3$ つが挙げられます。


全国数学高联竞赛论坛第一期 一道平面几何题的几种证明 金石为开教育公司



2 三角形的外接圓與外心角度 基本觀念 國三上3 2 Live數學學習網 Www Liveism Com 名師葛倫 Youtube
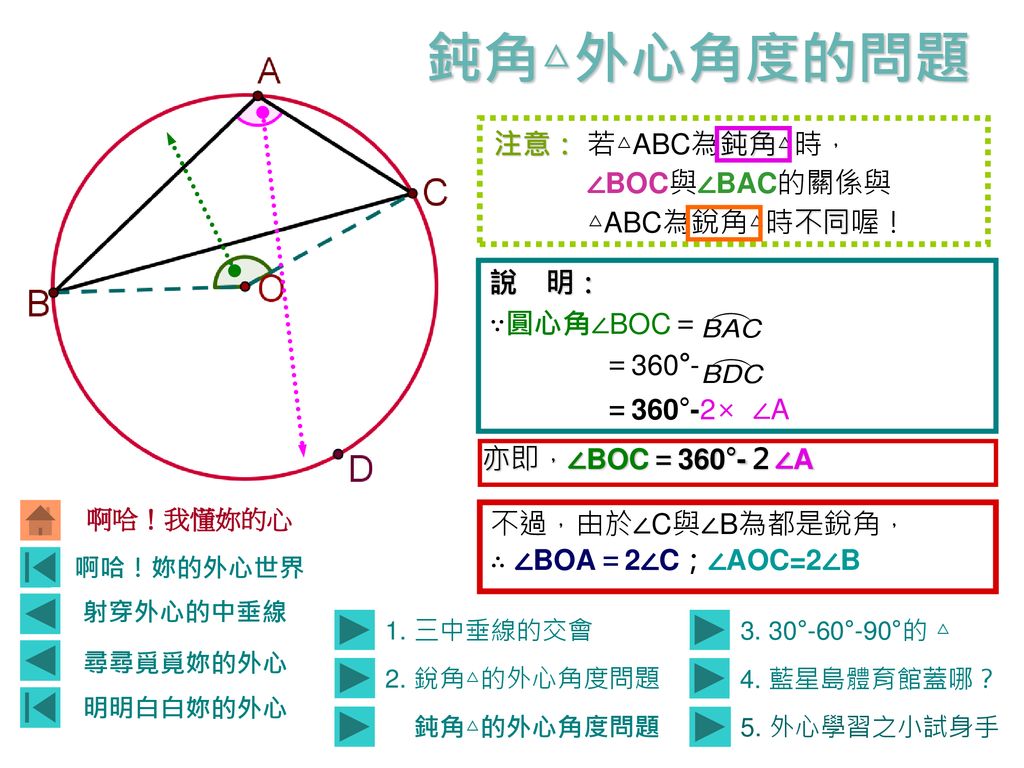
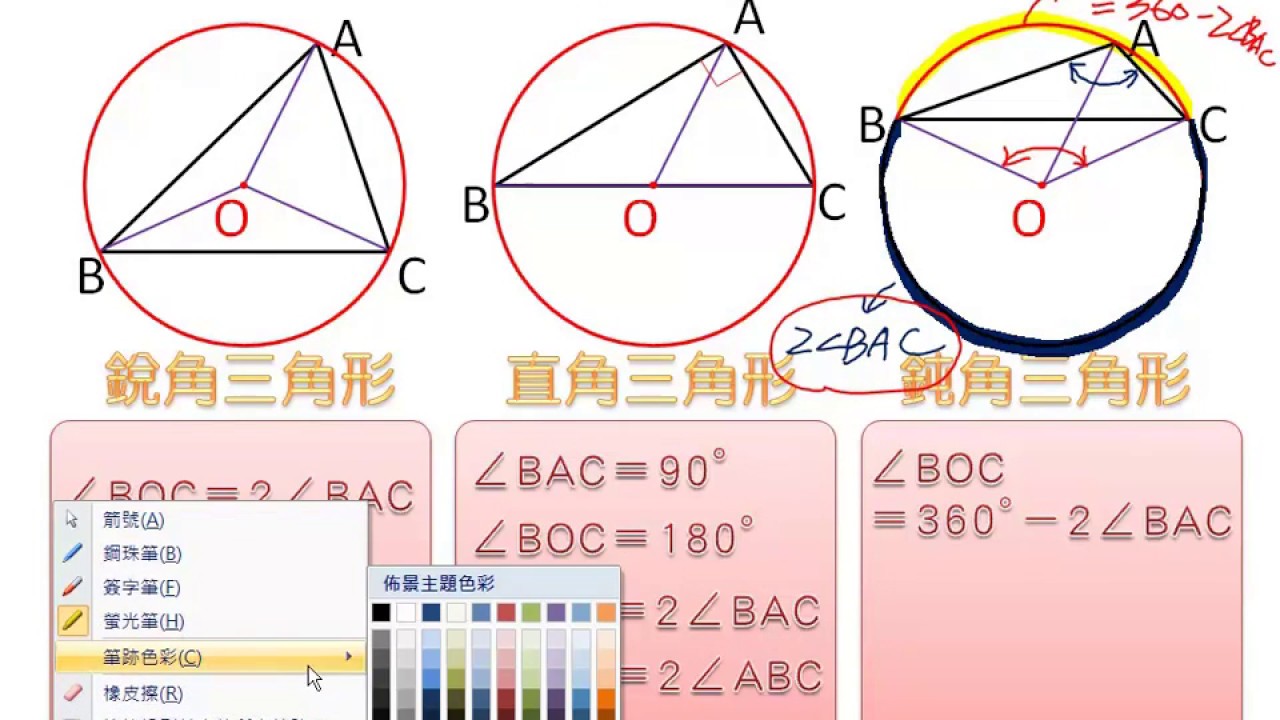
重要な相互関係 1 正三角形のときは,重心・外心・内心・垂心は一致します. 2 三角形の外接円の半径Rは,内接円の半径rよりも大きくなります.(2倍以上になります.)外心到三頂點等距離:若o為 abc的外心,則==。 外心的位置及角度問題:若o為 abc的外心 銳角 ,o在 內部 直角 ,o在斜邊中點 鈍角 ,o在 外部 ∠boc=2∠bac ∠boc=2∠bac=180∘ ∠boc=360∘-2∠bac 外心與 外接圓半徑:三角形の外心とは 外心 とは 三角形の外接円の中心 のことです。 三角形の各頂点から外心までの距離は半径にあたるため、すべて等しくなります。 外心は三角形の各辺における 垂直二等分線の交点 になります。 二等辺三角形が3つできることから、下の図のように〇、 、 の角は等しくなります。 鈍角三角形では外心は三角形の外部にできます。
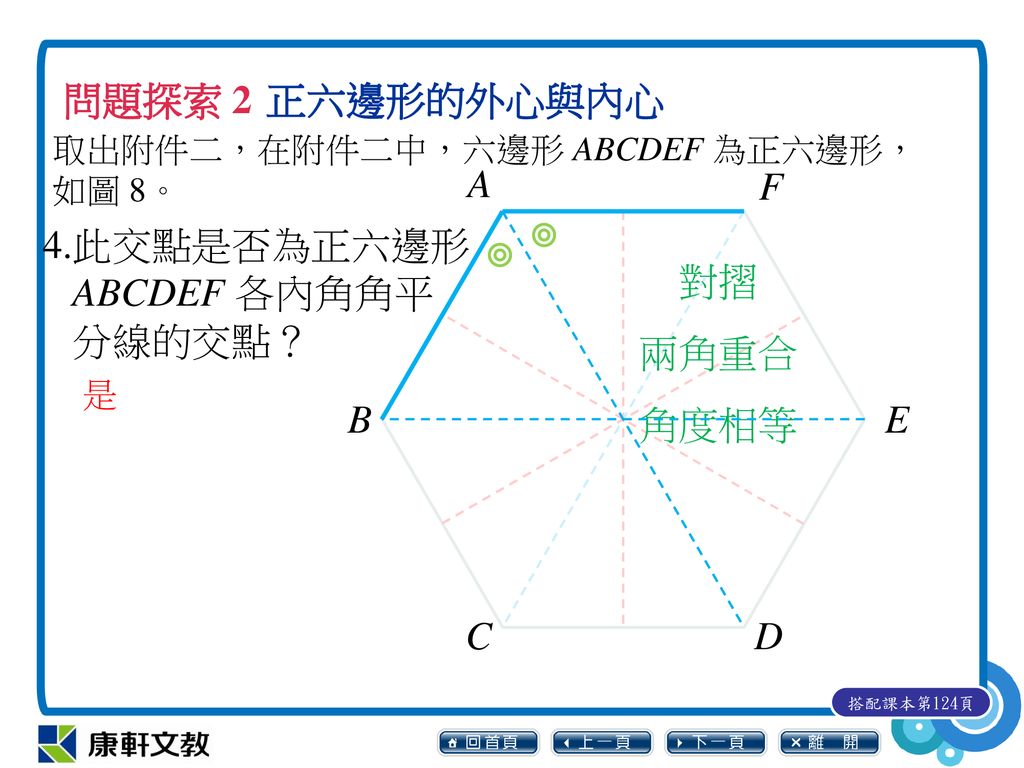


搭配課本第119頁 搭配課本第119頁圖1 搭配課本第119頁圖2 搭配課本第119頁 Ppt Download
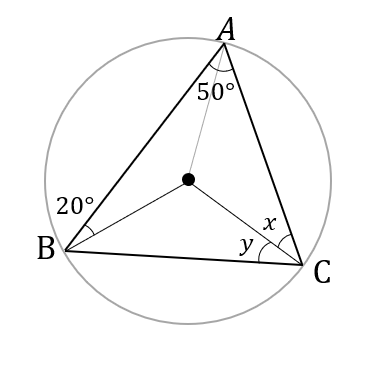


外心 内心 重心の特徴と問題の解き方をサクッとまとめ 数スタ
9/16/14 · ① 最短経路の問題 最上級問題 ⑭ 正四面体の平行移動 最上級問題 ⑧ 立方体の平行移動 最上級問題 (22) 2つの正方形 最上級問題 (21) 九角形の面積 最上級問題 ⑱ 立方体の共通部分 最上級問題 ⑬ 正八角形の問題About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How YouTube works Test new features Press Copyright Contact us CreatorsPage 1 高校で教えたい幾何の問題 メネラウスで三角形を巡る 札幌旭丘高校 中村文則 はじめに 平面幾何は補助線のヒラメキを解法の主たる要素とすることが多く,引き方如何により結論までの距離



Amc 10 第四讲 三角形的这4 颗心 我们要牢记在心 知乎
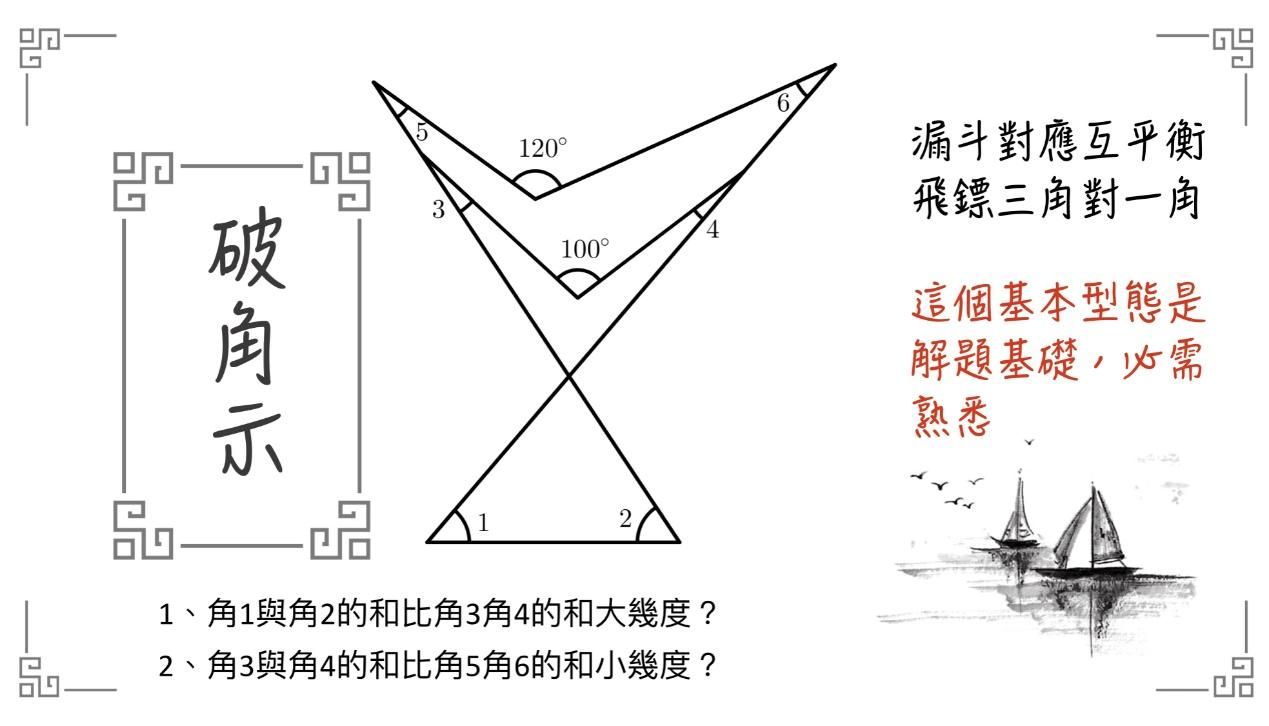


110會考衝刺 數學 熟練這9大題型 幾何題不再是失分題 翻轉教育 親子天下網站
長さを計算すると, しばしば角度のsinが長さ計算の過程で登場するので, 一 点で交わることを示す系の問題は, この問題を使うと良いことも多い また, こ の定理から等角共役点の存在が示せる また, 命題21を用いて, 次の系が示せる 系237/26/17 · 三角形の外心の話をする前に、垂直二等分線についておさらいをしておきましょう。 線分 AB があったとき、 AB の中点を通り、 AB と垂直に交わる線のことを、線分 AB の 垂直二等分線 (perpendicular bisector) といいます。 上の図で、線分 AB の中点を M としたとき、直線 PM が垂直二等分線になります。 なお、 AM = BM A M = B M, PM が共通、 ∠PMA = ∠PMB = 90∘ ∠ P M A =5// · 外心 外接円の中心 中線定理とは?定理の証明や問題の解き方をわかりやすく解説! 二等辺三角形とは?定義や定理、角度・辺の長さ・面積の求め方 微分方程式とは?解き方(変数分離など)や一般解・特殊解の意味
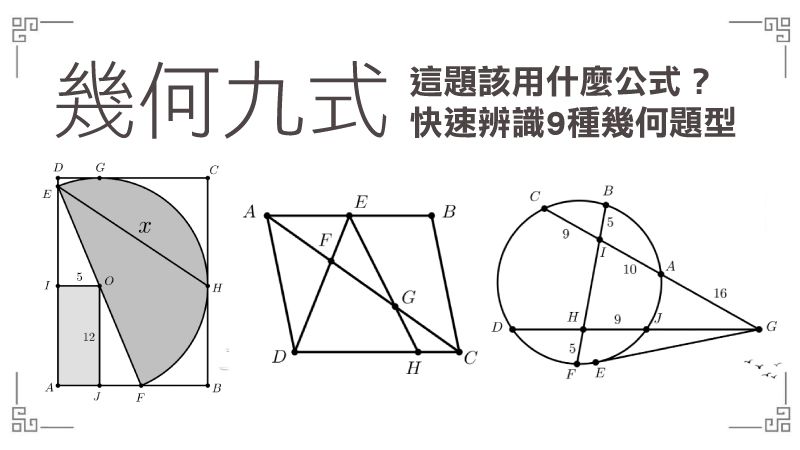


110會考衝刺 數學 熟練這9大題型 幾何題不再是失分題 翻轉教育 親子天下網站



外心 內心 重心的比較 Youtube
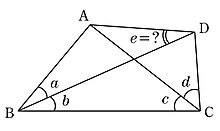
また、右図の整角四角形において、角度 a, b, c, d が与えられて角度 e を求める(または角度 e がその値となることを証明する)ような問題を整角四角形問題と呼ぶ。 ラングレーの問題は、整角四角形問題のうち ( a, b, c, d, e) = (, 60, 50, 30, 30) となるものに相当する。 一般の四角形では、 a, b, c, d がいずれも整数であっても、 e が整数となるとは限らない。 例えば ( a2/28/11 · 数学 この問題は αの角度を求める問題なんですが、答えが115゜になる意味が解りません(*_*) 私は100゜だと思っていました; ちなみにIは abcの内心だそうです。 回答お願いします。角度の問題 #29 解答例 →問題 で,ghを1辺とする正三角形xghをghから見てaと同じ側に作ると, gx=gh=gb=gcより,gは bcxの外心.



三角形とは 面積公式 角度 辺の長さ 重心 比の計算 受験辞典


外接円 外心について


八五年的乖乖 公司研究的核心是空间 结构 深度 角度 交易策略的核心是概率 赔率和预期差 投资体系的核心是对象


数aの角度の求め方を教えてください 点oは Abcの外心であ Yahoo 知恵袋
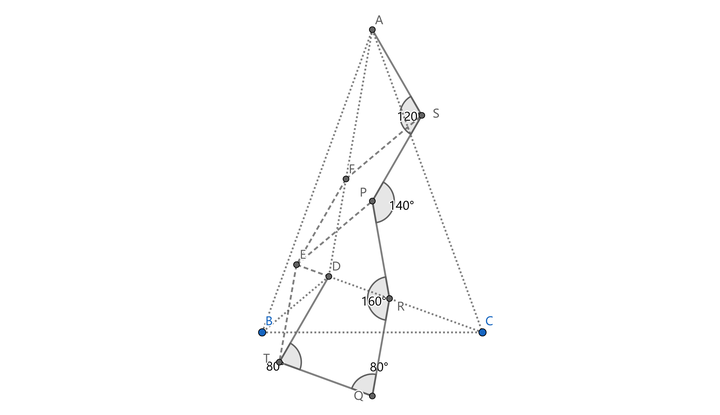


求大神解一下 这个三角形的度数怎么求 知乎


外心の基礎問題なんですが 解き方を忘れました yの角度の解き Yahoo 知恵袋


三角形的外心和頂角的關係 大川隆法書迷 愛情公寓交友網站與聊天室


名師課輔網 外心角度



啊哈 妳的外心世界如果你能懂我的外心世界 你就能解決這個問題喔 這是藍星上的藍星島 島上的三個大城市
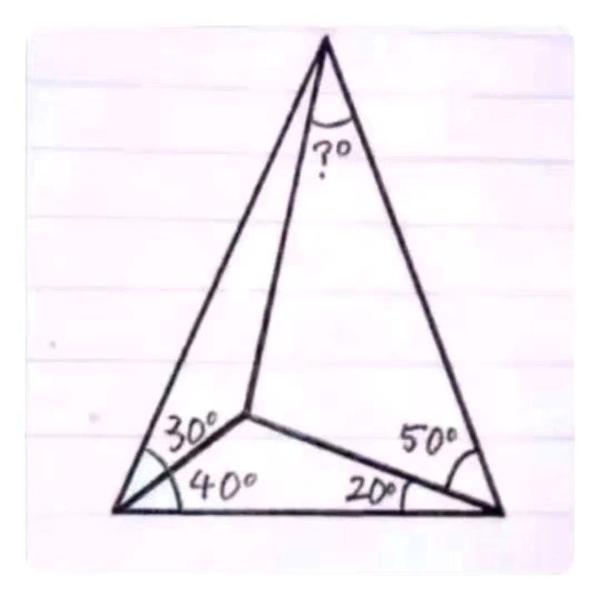


角格点 完全分类 知乎



必修四向量 三角形 重心 垂心 內心 外心 向量結論與證明 每日頭條



2 三角形的外接圓與外心角度 基本觀念 國三上3 2 Live數學學習網 Www Liveism Com 名師葛倫 Youtube



3d 数学基础 脑图笔记 404forest



Jiangsu Vedkang Medical Science And Technology Co Ltd Publicaciones Facebook


你是有多好命 才能娶到这个星座女


三角形的外接圓與外心角度 Live 多媒體數學觀念典online



搭配課本第119頁 搭配課本第119頁圖1 搭配課本第119頁圖2 搭配課本第119頁 Ppt Download



必修四向量 三角形 重心 垂心 內心 外心 向量結論與證明 每日頭條



衣


最新白菜网络论坛财经大学 会计学院 Www Gcs100 Com



责任心的重要性下载 Word模板 爱问共享资料
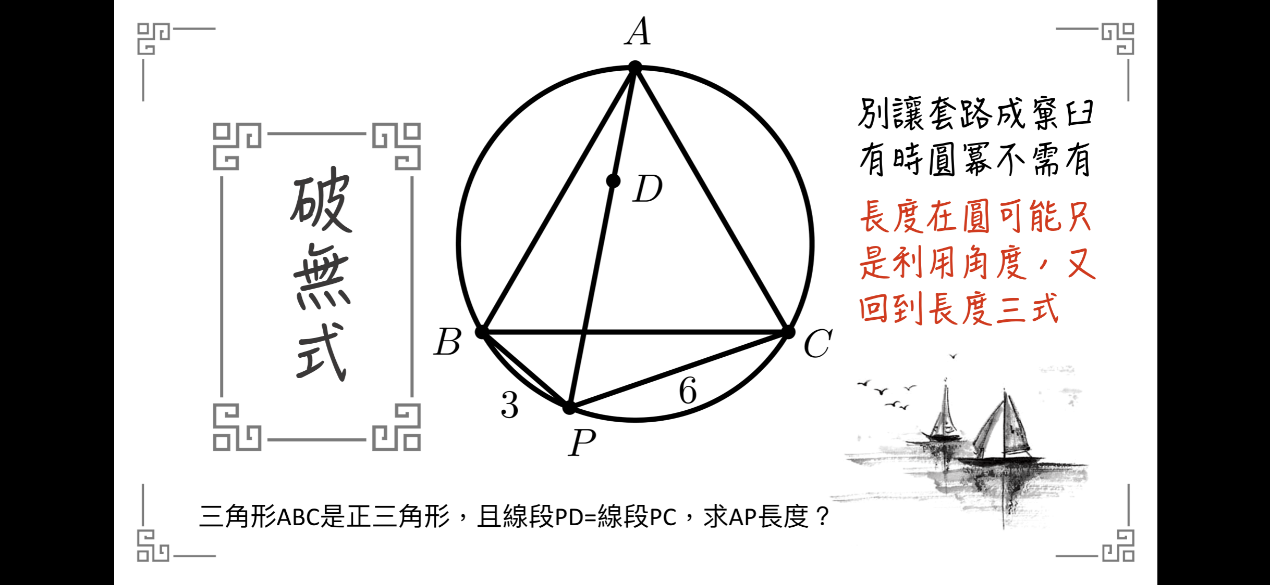


110會考衝刺 數學 熟練這9大題型 幾何題不再是失分題 翻轉教育 親子天下網站
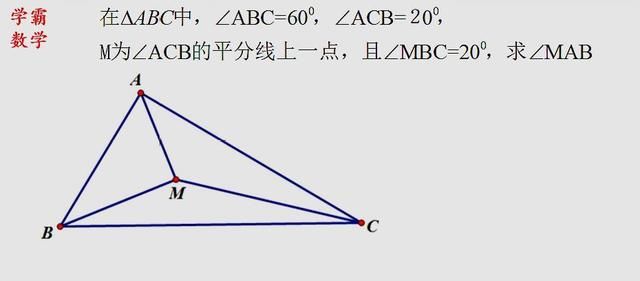


等腰三角形的内心和外心
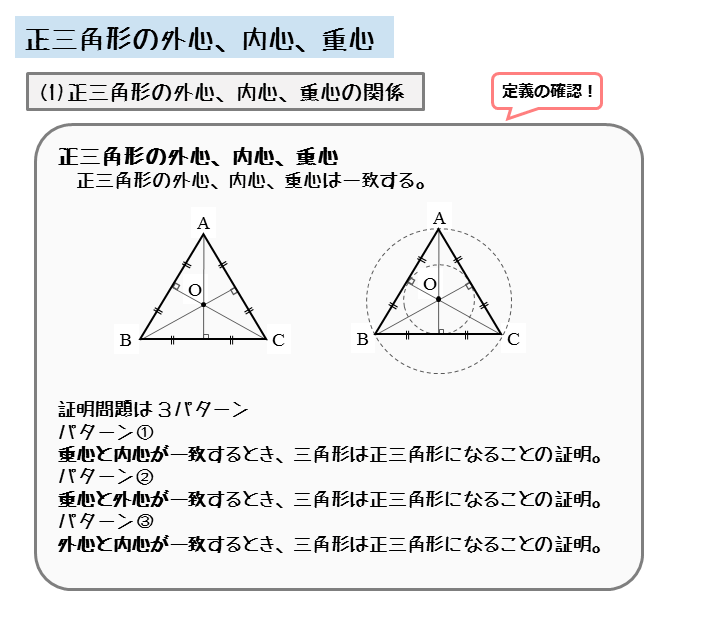


図形の性質 正三角形の外心 内心 重心について 日々是鍛錬 ひびこれたんれん


Amc 10 第四讲 三角形的这4 颗心 我们要牢记在心 知乎



必修四向量 三角形 重心 垂心 內心 外心 向量結論與證明 每日頭條



三角形的外接圓與外心角度 Live 多媒體數學觀念典online



三角形の外心について知っておきたい知識まとめ 理系ラボ


外接円 外心について



必修四向量 三角形 重心 垂心 內心 外心 向量結論與證明 每日頭條


初中三年的数学定理都在这了 暑假预习必备 赶快收藏 版权



必修四向量 三角形 重心 垂心 內心 外心 向量結論與證明 每日頭條



疫情日记六三二 21年入学难度增加 如何创造改变 项目真诚招募英才 美国厚仁教育


啊哈 妳的外心世界如果你能懂我的外心世界 你就能解決這個問題喔 這是藍星上的藍星島 島上的三個大城市



三角形の外心 高校数学a Youtube



点oが三角形abcの外心であるときのaの角度の求め方を教えてください Clear



夫妻相处不离修行 家庭就是彼此的修炼场 婚姻 结婚 佛法 网易订阅



啊哈 妳的外心世界如果你能懂我的外心世界 你就能解決這個問題喔 這是藍星上的藍星島 島上的三個大城市



外心とは 三角形の外心の座標 位置ベクトルの求め方や性質の証明をわかりやすく解説 垂心 遊ぶ数学塾



东方阳熹 王凤仪性命哲学浅述 第三篇 四大界 5 2 Youtube


角格点 完全分类 知乎



Days To Go 1 Days 四心提提你 數學補習 Dse補數學 中學數學專科補習社



必修四向量 三角形 重心 垂心 內心 外心 向量結論與證明 每日頭條


兰利的不定角度问题 维基百科 自由的百科全书



外心とは 三角形の外心の座標 位置ベクトルの求め方や性質の証明をわかりやすく解説 垂心 遊ぶ数学塾
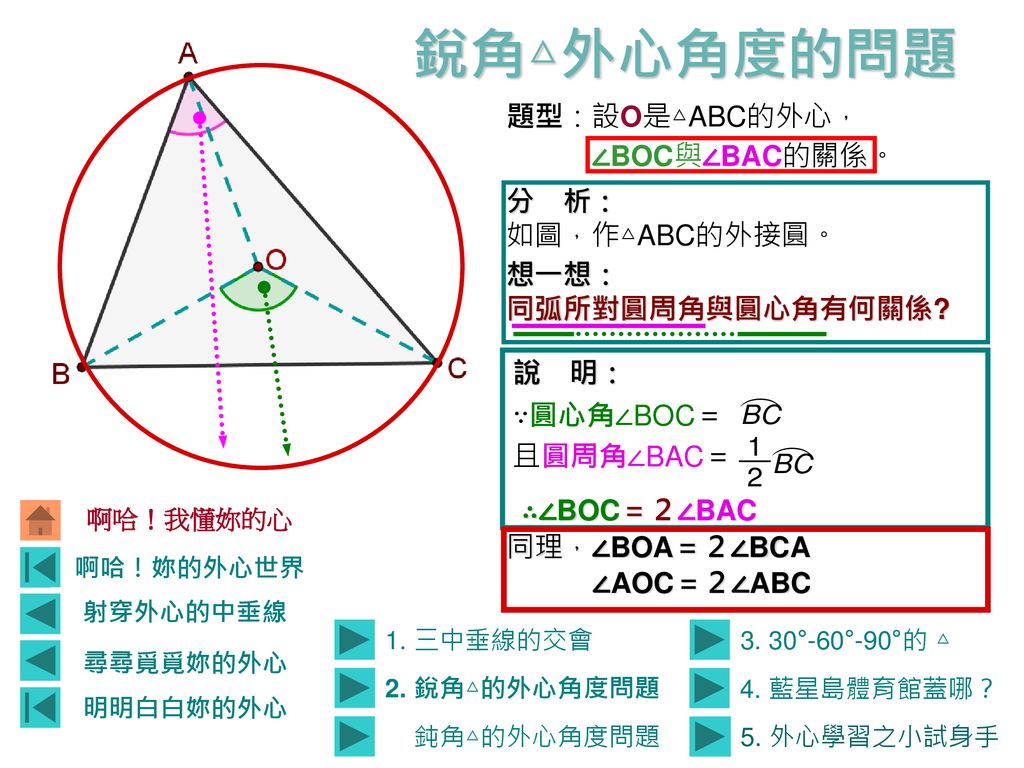


啊哈 妳的外心世界如果你能懂我的外心世界 你就能解決這個問題喔 這是藍星上的藍星島 島上的三個大城市



角度問題 外心 內心の基本問題 角度 翻譯此網頁 ury



三角形の外心 内心 重心 垂心 Geogebra


Amc 10 第四讲 三角形的这4 颗心 我们要牢记在心 知乎



三角形的外接圓與外心角度 Live 多媒體數學觀念典online


Ppt 三角形的外心powerpoint Presentation Free Download Id


啊哈 妳的外心世界如果你能懂我的外心世界 你就能解決這個問題喔 這是藍星上的藍星島 島上的三個大城市
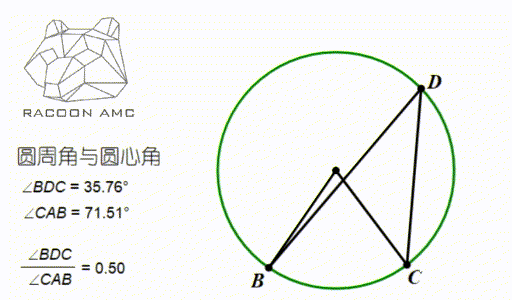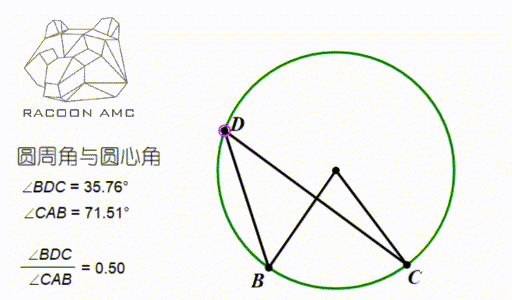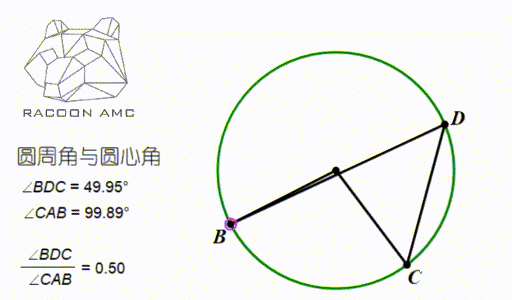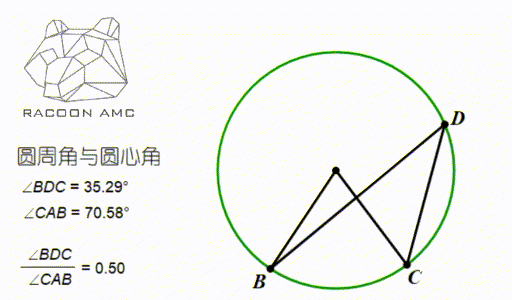


Amc 10 第五讲 圆中的角度和长度 知乎



外心とは 三角形の外心の座標 位置ベクトルの求め方や性質の証明をわかりやすく解説 垂心 遊ぶ数学塾


数学aの角度を求める問題について教えて下さい 問16 abcの外 Yahoo 知恵袋



Knkhcrlthbim



大咖分享 一个求角度问题的多种解法 平行线教育官网



头条文章



2 三角形的外接圓與外心角度 基本觀念 國三上3 2 Live數學學習網 Www Liveism Com 名師葛倫 Youtube
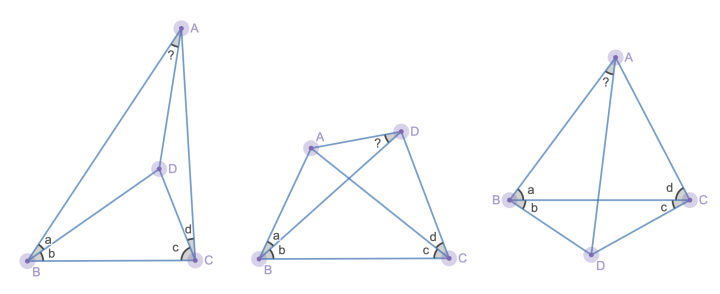


角格点 完全分类 知乎


三角形の外心 角度 三角形の外心の角度の問題おしえてください 画像を添 Yahoo 知恵袋



怎样只用圆规找到一个三角形的内心 知乎



必修四向量 三角形 重心 垂心 內心 外心 向量結論與證明 每日頭條


外接円 外心について



例題4 3 2 三角形內心的角度問題 Youtube


兰利的不定角度问题 维基百科 自由的百科全书



疫情日记六三二 21年入学难度增加 如何创造改变 项目真诚招募英才 美国厚仁教育



8种方法解决一道三角形中角格点经典问题 题型虽老 但仍有价值 外接圆 外心 共圆 网易订阅



Amc 10 第五讲 圆中的角度和长度 知乎


Amc 10 第四讲 三角形的这4 颗心 我们要牢记在心 知乎



高1数学a平面図形 この問題を教えてください Oは外心a Bの角度を求 数学 教えて Goo



三角形的外接圓與外心角度 Live 多媒體數學觀念典online


2 三角形的外接圓與外心角度 基本觀念 國三上3 2 Live數學學習網 Www Liveism Com 名師葛倫 Youtube


啊哈 妳的外心世界如果你能懂我的外心世界 你就能解決這個問題喔 這是藍星上的藍星島 島上的三個大城市



换个角度看人生的图片 第1页 一起扣扣网
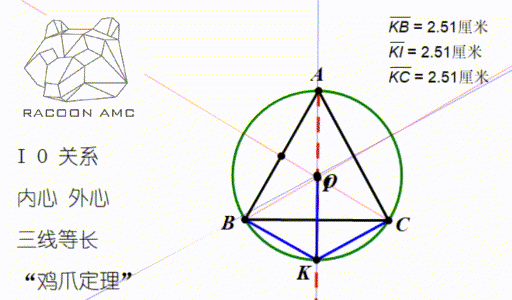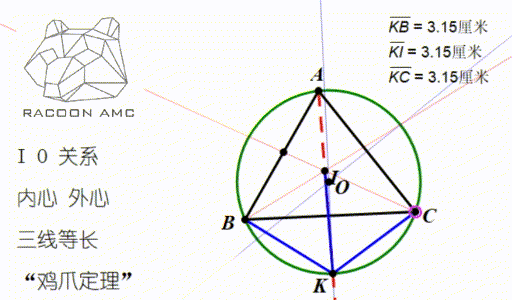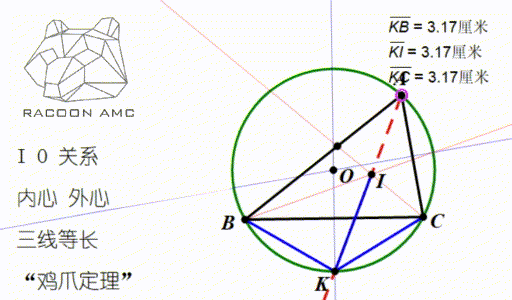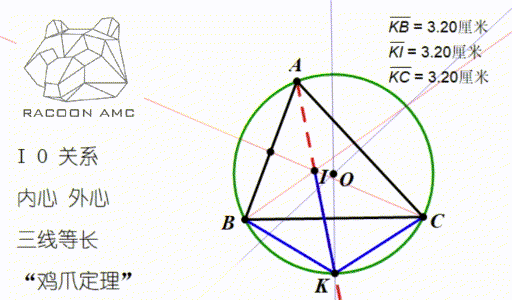


Amc 10 第四讲 三角形的这4 颗心 我们要牢记在心 知乎


光纤弯折会影响网速吗 多少角度合适 弱电课堂 微信公众号文章阅读 Wemp



数学です 重心 内心 外心です わかる方教えてください 数学です 数学 教えて Goo



0 件のコメント:
コメントを投稿